Band unfolding of twisted bilayer graphene
QuanSheng Wu
École Polytechnique Fédérale de Lausanne (EPFL), Switzerland
(Dec. 9. 2019)
Here we present an example to show how to unfold energy band from a pristine cell to a target cell within WannierTools [1] . There are two conditions that should be satisfied. 1. The pristine cell should be larger than the target cell. 2. The lattice vectors of the pristine cell should be representable by the lattice vectors of the target cell.
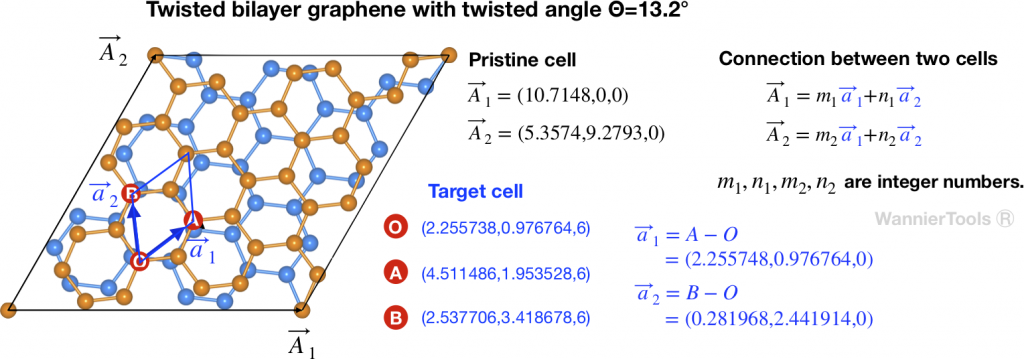
Let’s take twisted bilayer graphene (TBG) as an example. The crystal structure is presented in Fig 1.
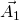 ,
, 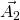 ,
, 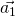 and
and 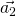 should be defined in the same cartesian coordinates.
should be defined in the same cartesian coordinates.TBG is consist with two graphene sheets with a twisted angle. In order to compare the energy bands between TBG and graphene, we need to unfold the energy bands of TBG to the Brillouin zone of Graphene. In Fig 1, ![]() ,
, ![]() (
(![]() ,
, ![]() ) are lattice vectors of pristine (target) cell. They are related by
) are lattice vectors of pristine (target) cell. They are related by ![]() ,
, ![]() , where
, where ![]() are integer numbers. The connection between pristine and target cells are necessary information. So we need to define them in the input file of WannierTools wt.in.
are integer numbers. The connection between pristine and target cells are necessary information. So we need to define them in the input file of WannierTools wt.in.
LATTICE_UNFOLD ! should have the same coordinates as LATTICE
Angstrom
2.255748 0.976764 0.0000000
0.281968 2.441914 0.0000000
0.000000 0.000000 20.000000
ATOM_POSITIONS_UNFOLD
2
Direct ! Direct means the fractional coordinations based on LATTICE_UNFOLD
C 0.000000 0.000000 0.300000
C 0.666667 0.666667 0.300000
PROJECTORS_UNFOLD
2*1 ! number of projectors
C pz
C pz
SELECTED_ATOMS
1
1-38 ! indices defined in the ATOM_POSITIONS
For TBG, it’s important to define the SELECTED_ATOMS since so that the selected atoms are in the layer that define the LATTICE_UNFOLD and ATOM_POSITIONS_UNFOLD. Otherwise there will be ghost bands [2] .
There are two modes to get the unfolded spectrum in WannierTools. One is to get the band structure along some selected k paths (KPATH_BULK). The other one is to get a energy contour plot with a given energy E_arc and a k plane (KPLANE_BULK). They are controlled by BulkBand_Unfold_plane_calc and BulkBand_Unfold_plane_calc in the CONTROL namelist of wt.in.
For example, Fig. 2 shows the pristine bands and the unfolded bands of TBG with twisted angle ![]() .
.
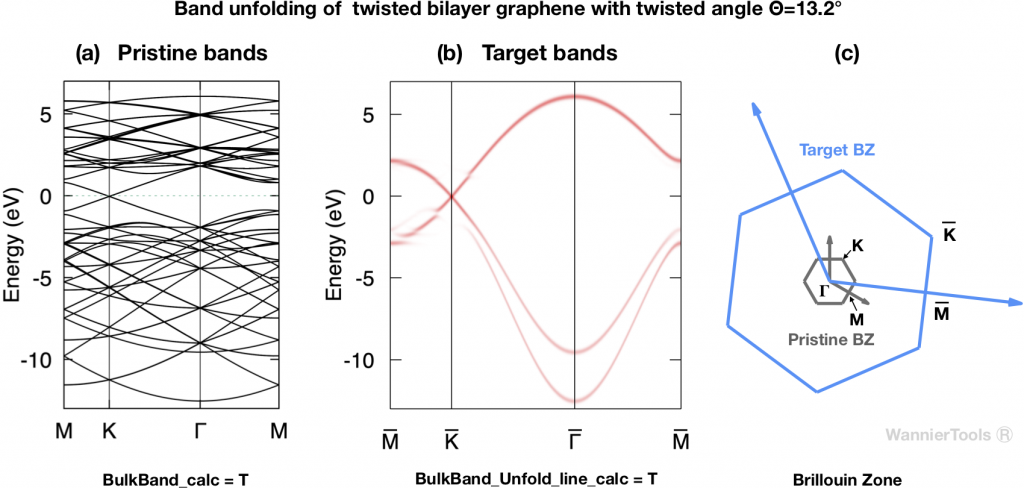
The relevant parameters for generating Fig.2 in wt.in are
!> bulk band structure calculation flag
&CONTROL
BulkBand_calc = T
BulkBand_Unfold_line_calc = T
/
&PARAMETERS
Eta_Arc = 0.050 ! infinite small value, like brodening
E_arc = 1.00 ! energy contour plot
OmegaNum_unfold =600 ! energy slices for Fig. 2(b)
OmegaMin = -13.0 ! energy interval
OmegaMax = 7.0 ! energy interval
Nk1 =201 ! number k points
Nk2 =201 ! number k points
/
KPATH_BULK ! k point path
3 ! number of k line only for bulk band
M 0.00000 0.50000 0.00000 K 0.33333 0.66667 0.00000
K 0.33333 0.66667 0.00000 G 0.00000 0.00000 0.00000
G 0.00000 0.00000 0.00000 M 0.00000 0.50000 0.00000
Other necessary parameters can be found in the example folder /path-to-wann_tools/examples/TBG-13.2degree/
References:
[1] WannierTools: An open-source software package for novel topological materials, QuanSheng Wu and ShengNan Zhang and Hai-Feng Song and Matthias Troyer and Alexey A. Soluyanov, Computer Physics Communications 224, 405 (2018)
[2] Band-unfolding approach to moiré-induced band-gap opening and Fermi level velocity reduction in twisted bilayer graphene, Hirofumi Nishi, Yu-ichiro Matsushita, and Atsushi Oshiyama, PHYSICAL REVIEW B 95, 085420 (2017)